Some game systems make use of open ended dice rolling - that is, everytime you roll the max you get to roll again adding to the total. If the system called for you to roll 2d6 open ended you could conceivably roll:
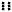
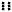
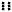
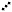
for a grand total of 23.
This got me wondering about how to calculate the average value that an open ended roll produces. For example, we all know that the average value produced by rolling a d6 is 3.5 ... but what is the average value produced by rolling a d6 open ended? And what is the value for other dice types?
So ... after fiddling around with numbers on some scratch paper for a little bit I think I've found a general formula. I'm sure that this site has some grognards who *know* the answer for sure and I'm hopeing some will see this post and can tell me if I'm right or correct me if not.
Anyway, my belief is that the general function for the average open ended roll of an n-sided dice is: n/2 + n/(n-1)
For a six sided dice, that formula produces a result of 4.2 - and funny enough that's the value I get from a computer program I wrote a long time ago to sim open ended d6 roles.
The first part of the formula (n/2) is the average for the terminator roll, the one that failed to carry the series forward.
The second part represents the contribution of the max value chaining along. So we have that max value * the average length of the chain. I aver (and I have only some sketchy scribbled calculations and faith to back it up) that the average length of chain of events with a probability of 1/n approaches 1/(n-1) as you push towards infinity.
So ... am I right?
for a grand total of 23.
This got me wondering about how to calculate the average value that an open ended roll produces. For example, we all know that the average value produced by rolling a d6 is 3.5 ... but what is the average value produced by rolling a d6 open ended? And what is the value for other dice types?
So ... after fiddling around with numbers on some scratch paper for a little bit I think I've found a general formula. I'm sure that this site has some grognards who *know* the answer for sure and I'm hopeing some will see this post and can tell me if I'm right or correct me if not.
Anyway, my belief is that the general function for the average open ended roll of an n-sided dice is: n/2 + n/(n-1)
For a six sided dice, that formula produces a result of 4.2 - and funny enough that's the value I get from a computer program I wrote a long time ago to sim open ended d6 roles.
The first part of the formula (n/2) is the average for the terminator roll, the one that failed to carry the series forward.
The second part represents the contribution of the max value chaining along. So we have that max value * the average length of the chain. I aver (and I have only some sketchy scribbled calculations and faith to back it up) that the average length of chain of events with a probability of 1/n approaches 1/(n-1) as you push towards infinity.
So ... am I right?




