WOIN probabilities of success

[Cat in the Hat]

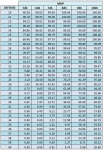
For my own game I have created a handy chart which lists the probabilities of success for the various number of dice and difficulties (inclusive of the chance of rolling triple sixes). Would other people find this useful? and if so, where can I upload it?

 

[TheHirumaChico]

I just downloaded it, and I know it will be tremendously helpful for me, many thanks CitH! I've been using an online dice calculator up until now, but having this as a handy reference is great!

 

[Morrus]

It’s pretty cool. But the chances of rolling 22 on 10d6, while high, aren’t 100%!

 

[TheHirumaChico]

Hmmm, good point. I didn't do any actual proofreading myself, just delighted to have a reference table like this.

 

[TheHirumaChico]

Maybe change all the "100%" entries to ">99%"?

 

[M3woods]

I've made a chart for personal use some time ago. I went two digits beyond the decimal for those smaller incremental changes to odds.

 

[TheHirumaChico]

Thanks, also very useful! @M3woods: Does your version also consider auto-success with a critical hit of three sixes?

 

[M3woods]

Thanks, also very useful! @M3woods: Does your version also consider auto-success with a critical hit of three sixes?

It does not include auto-successes. I'm not even sure how to calculate that but it's definitely something I'll look into.

 

[Cat in the Hat]

It’s pretty cool. But the chances of rolling 22 on 10d6, while high, aren’t 100%!

Yeah I should have mentioned that it it only accurate to +/- 1%. But rolling 22 on 10d6 is closer to 100% than 99% once you take into account an auto success from three sixes

 

[Cat in the Hat]

It does not include auto-successes. I'm not even sure how to calculate that but it's definitely something I'll look into.

I calculated it by treating the chance of a normal success and the chance of three sixes as independent events. Which they’re not. Which is why it’s only accurate to +/- 1%