Success chances for Skill Challenges

[Stalker0]

Mmm, I don't know what you mean here.

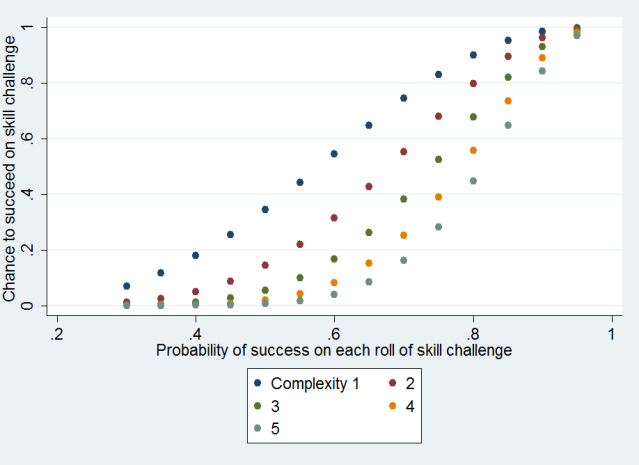
This calculation takes into account the success chance of a roll.
It doesn't account for skill bonuses or DCs.

You mean that it is rare that a party has always the same chance for each roll accross a SC?

What I mean is there is actually a lot of variance each roll for a skill challenge.

For example, let's say perception and athletics are both high difficulty skills for a challenge, so they have the same DC. Assuming both fighter and ranger have the same base good stats in their respective skills, the ranger might have a +7 bonus advantage over the fighter (+3 for skill focus, -2 to the fighter for his ACP if he's in plate, or -4 if he's in plate,heavy shield).

Further, if players choose different skills each round, their bonus may once again shift.

Finally, and this one is the hardest one to compensate for mathematically I have found, is there are a huge number of powers that provide bonuses to skill rolls. For example, my party's wizard has a utility power that lets him reroll an arcana check once per encounter. That is actually a huge bonus on a single roll for for a skill challenge.


So when the model simply assumes everyone in the party has a 65% chance to make their rolls for a round, that is really underestimating the complexity of the system.

 

[Stalker0]

I think you can do the calculations more easily by simply summing the probabilities of failures. It actually doesn't matter what the sequence of rolls is. So for complexity 1 its 7 rolls with less than 3 failures. So all you need to know is the chance in 7 rolls of 3 dice coming up below N. That number is 7/(21-N)*.05 + 6/(21-N)*.05 + 5/(21-N)*.05 is it not?

With the normal skill challenge, this doesn't work.

Skill Challenges actually care about who goes first.

Just for the sake of example, let's assume I have 7 players. 4 of them have great skill bonuses for a challenge, and 3 have terrible ones.

If the 4 players go first and all make their rolls, the challenge is a success. The 3 other players bonuses actually didn't factor into the skill challenge at all.

If the 3 players go first and fail, the challenge is a failure, the 4 players bonuses had no affect.


In most cases in a skill challenge, you won't get to make 7 rolls. The challenge will be won or lost before that, so modeling probability assuming 7 rolls occures each time results in inaccurate math.

 

[Elric]

With the normal skill challenge, this doesn't work.

Skill Challenges actually care about who goes first.

Just for the sake of example, let's assume I have 7 players. 4 of them have great skill bonuses for a challenge, and 3 have terrible ones.

If the 4 players go first and all make their rolls, the challenge is a success. The 3 other players bonuses actually didn't factor into the skill challenge at all.

If the 3 players go first and fail, the challenge is a failure, the 4 players bonuses had no affect.

In most cases in a skill challenge, you won't get to make 7 rolls. The challenge will be won or lost before that, so modeling probability assuming 7 rolls occurs each time results in inaccurate math.

You don't need to condition on the exact sequence of rolls for skill challenges. The key is that a skill challenge of S successes before F failures can only last S+F-1 rolls. E.g., 4 successes before 3 failures. After 6 rolls, you'll either have 4+ successes (and 0-2 failures), or you'll have <=3 successes and 3+ failures. It looks like order matters when you look at the 7th roll, but that roll isn't going to matter!

It's equivalent to a normal 4 S/3 F skill challenge to assume you make six rolls, regardless of the outcomes, and then decide on success or failure of the challenge (>=4 successes-> success, >=3 failures -> fail). If you already got to 4 successes, you can't possibly reach 3 failures in six rolls, and vice versa (this isn't true if you consider the 7th roll). So order doesn't matter in the first six rolls, and you ignore all rolls after that.

As a result, calculating the chance to succeed on a skill challenge is simple when the chance to succeed on each roll is the same. It's the chance that in (S+F-1) trials, each with a probability p of success, you get <F failures. This is an application of the Binomial distribution

 

[Elric]

Here's a graph of the chance to succeed on a skill challenge as a whole (the y-axis) when you have a constant chance of success on each of the rolls in a skill challenge (the x-axis), calculated for skill challenges of complexity 1-5 (the different colors of data points). Note that a Complexity k skill challenge is 2k +2 successes before 3 failures. sfedi had a list of these results earlier in the thread, but I'm a big fan of presenting information using graphs.

 

[sfedi]

Wow! Great graph! MUCH more clearer.

Thanks Elric!

 

[AbdulAlhazred]

You don't need to condition on the exact sequence of rolls for skill challenges. The key is that a skill challenge of S successes before F failures can only last S+F-1 rolls. E.g., 4 successes before 3 failures. After 6 rolls, you'll either have 4+ successes (and 0-2 failures), or you'll have <=3 successes and 3+ failures. It looks like order matters when you look at the 7th roll, but that roll isn't going to matter!

It's equivalent to a normal 4 S/3 F skill challenge to assume you make six rolls, regardless of the outcomes, and then decide on success or failure of the challenge (>=4 successes-> success, >=3 failures -> fail). If you already got to 4 successes, you can't possibly reach 3 failures in six rolls, and vice versa (this isn't true if you consider the 7th roll). So order doesn't matter in the first six rolls, and you ignore all rolls after that.

As a result, calculating the chance to succeed on a skill challenge is simple when the chance to succeed on each roll is the same. It's the chance that in (S+F-1) trials, each with a probability p of success, you get <F failures. This is an application of the Binomial distribution

True. You roll SuccessesRequired+2 dice and if there are less than 3 fails in those dice then the residual chance of failure is the toss of the final die. In order to consider different character's with different success probabilities is actually simple enough, you just assign different probabilities to each die. It doesn't actually matter which die is that last die either since the whole challenge is essentially order independent.

EDIT: Sorry. This is what happens when you think about it for 1 minute too few... On complexity 1 you never need more than 6 tosses to determine if the party succeeded or not. These dice can be thrown in parallel. Thus your code can be parallelized. Assuming you have more than one core on your CPU multiple dice can be tossed at one time, if you have a single core processor then backtracking is equally efficient. So essentially both you and Stalker0 are correct, its just that your way of looking at it can lead to a more efficient code solution if you have the proper hardware.

Create a threadpool, drop SuccessesRequired+2 die rolling jobs into the pool. Sum the fails and if its <2 its a failed challenge, otherwise its a successful challenge. On a single core processor it won't be faster than backtracking, but on a multicore machine it should give you a bit quicker answer. That would be the Monte-Carlo method. You can also simply sum the probabilities and get a statistical answer, still uses the same number of dice, which is a binomial distribution.

I could work up a piece of code, but then again I'm sure any of us can do that... lol.