D&D General Replacing 1d20 with 3d6 is nearly pointless
- Thread starter NotAYakk
- Start date
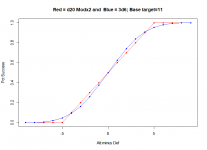
I think the d20 where you multiply the attack and defense mods by 2 and set the base target number to 11 came out identical to the d10+5 with base 11.
In the d20 mult 2 base 11 the only possible target numbers are odd, so getting the target odd or the even right above it are the same effect. (And the graph is the probability of success on the roll).
Let me know if that doesn't sound right.
Laugh, of course.
I was just amused/confused by the fact there are 10 points.
Anyhow, it is sort of amazing how close the strait line comes to the curve. When I first graphed it I thought I made a mistake.
The tails, as you noted, are different; that is why I keep on saying "outside of crit hit/miss mechanics", because the tails are basically 5% chance on either side.
If you change the graph so that 1 loses to everything, and 20 beats everything, and then take the 3d6 and make it so that 17-18ish auto-succeeds and 3-4ish auto-fails, the tails even look similar.
You think you were confused, you should have seen me double checking code last night after my usual bed-time.
Garthanos
Arcadian Knight
That might be the goal... ie to make the choice based elements more significant than the random
So, a point is only made if everyone on the planet hears it at the time and agrees for the rest of history?
That's an... interesting take on making points.
Ahhh... The argument is:
"You can't tell the difference in your average game because the results are still within the same range."
Took a long time to discern that, I apologize. And in that case I say "I suppose that depends on how you're playing."
In the games where I played with 3d6 instead of 1d20 it was fairly evident in the long run because I was in Job Corps doing all night every night D&D and GURPS after class. Over a hundred rolls every day for weeks at a time in 6-16 hour sessions (depending on the day of the week) made it suuupes obvious that 3d6 weighted toward the middle and shaped the way the game felt.
To the point that I would run 3d6 3e and 3.5e D&D for years to come while my at-the-time boyfriend shunned it in favor of the swingier d20 and played it all up for slapstick DBZ style comedy on Nat 1s.
That said, you can always load up AnyDice to get a randomized sample... how many rolls would you say the average session has? 4 players and 5 monsters, monsters survive 3 rounds. Everyone gets one roll a turn, but also saves happen so on some turns multiple people have to roll an AoE save...
Let's call it 30 rolls over the course of the fight, including 9 initiatives.
30 rolls with 1d20: 17, 5, 11, 14, 15, 14, 19, 11, 8, 19, 18, 14, 1, 10, 9, 13, 13, 7, 5, 9, 3, 16, 4, 4, 11, 13, 19, 6, 7, 12
1) 1
2) 0
3) 1
4) 2
5) 2
6) 1
7) 1
8) 1
9) 1
10) 1
11) 3
12) 1
13) 3
14) 3
15) 1
16) 1
17) 0
18) 1
19) 2
20) 0
30 rolls with 3d6: 15, 12, 12, 6, 7, 11, 11, 13, 13, 6, 13, 11, 12, 15, 10, 11, 12, 12, 13, 13, 9, 11, 13, 10, 14, 7, 7, 8, 16, 10
3) 0
4) 0
5) 0
6) 1
7) 3
8) 1
9) 1
10) 3
11) 5
12) 5
13) 4
14) 1
15) 1
16) 0
17) 0
18) 0
In even a single fight the weighting is really strong and evident.
I used AnyDice to provide the rolls.
"You can't tell the difference in your average game because the results are still within the same range."
Took a long time to discern that, I apologize. And in that case I say "I suppose that depends on how you're playing."
In the games where I played with 3d6 instead of 1d20 it was fairly evident in the long run because I was in Job Corps doing all night every night D&D and GURPS after class. Over a hundred rolls every day for weeks at a time in 6-16 hour sessions (depending on the day of the week) made it suuupes obvious that 3d6 weighted toward the middle and shaped the way the game felt.
To the point that I would run 3d6 3e and 3.5e D&D for years to come while my at-the-time boyfriend shunned it in favor of the swingier d20 and played it all up for slapstick DBZ style comedy on Nat 1s.
That said, you can always load up AnyDice to get a randomized sample... how many rolls would you say the average session has? 4 players and 5 monsters, monsters survive 3 rounds. Everyone gets one roll a turn, but also saves happen so on some turns multiple people have to roll an AoE save...
Let's call it 30 rolls over the course of the fight, including 9 initiatives.
30 rolls with 1d20: 17, 5, 11, 14, 15, 14, 19, 11, 8, 19, 18, 14, 1, 10, 9, 13, 13, 7, 5, 9, 3, 16, 4, 4, 11, 13, 19, 6, 7, 12
1) 1
2) 0
3) 1
4) 2
5) 2
6) 1
7) 1
8) 1
9) 1
10) 1
11) 3
12) 1
13) 3
14) 3
15) 1
16) 1
17) 0
18) 1
19) 2
20) 0
30 rolls with 3d6: 15, 12, 12, 6, 7, 11, 11, 13, 13, 6, 13, 11, 12, 15, 10, 11, 12, 12, 13, 13, 9, 11, 13, 10, 14, 7, 7, 8, 16, 10
3) 0
4) 0
5) 0
6) 1
7) 3
8) 1
9) 1
10) 3
11) 5
12) 5
13) 4
14) 1
15) 1
16) 0
17) 0
18) 0
In even a single fight the weighting is really strong and evident.
AnyDice
AnyDice is an advanced dice probability calculator, available online. It is created with roleplaying games in mind.
anydice.com
I used AnyDice to provide the rolls.
No, it isn't 30 rolls with 1d20 vs 30 rolls with 3d6 with the values recorded.
It is 30 rolls with 5.25+1d20/2 vs 30 rolls with 3d6 with only the success/failure recorded, and natural 1/20 being auto-fail/success, and 3-4 on 3d6 being auto fail, and 17-18 being auto success.
(This is just the math that mimics "double modifiers and DCs")
In D&D, you don't care if you roll 17 exactly. You care if you beat a DC. The process of "do you beat the DC" converts the distribution you care about from the "chance of X" to "chance of >= X" -- takes the cumulative distribution function of your probability. This is an integration operation, and the integration operation smooths the bell curve and makes it, well, look more like a strait line.
and that is the graph of this d20 vs 3d6 chances to beat various DCs, without any "auto succeed/fail at max/min roll" critical hit/miss system. Adding a critical hit/miss system would take the red line and stop it at 0.05 and 0.95, and probably do something similar for the 3d6 (do crits happen at 18? 17? 16? Do fumbles happen at 3, 4, 5?)
Generate a game with a distribution of DCs that is plausible, even known. Now have 100 rolls. See if you can make a statistical test that will reliably detect which is which.
If you are looking for a different system for crit hits/misses, that is one thing. But in the middle, 3d6 is just ... paint on the Porsche.
It is 30 rolls with 5.25+1d20/2 vs 30 rolls with 3d6 with only the success/failure recorded, and natural 1/20 being auto-fail/success, and 3-4 on 3d6 being auto fail, and 17-18 being auto success.
(This is just the math that mimics "double modifiers and DCs")
In D&D, you don't care if you roll 17 exactly. You care if you beat a DC. The process of "do you beat the DC" converts the distribution you care about from the "chance of X" to "chance of >= X" -- takes the cumulative distribution function of your probability. This is an integration operation, and the integration operation smooths the bell curve and makes it, well, look more like a strait line.
and that is the graph of this d20 vs 3d6 chances to beat various DCs, without any "auto succeed/fail at max/min roll" critical hit/miss system. Adding a critical hit/miss system would take the red line and stop it at 0.05 and 0.95, and probably do something similar for the 3d6 (do crits happen at 18? 17? 16? Do fumbles happen at 3, 4, 5?)
Generate a game with a distribution of DCs that is plausible, even known. Now have 100 rolls. See if you can make a statistical test that will reliably detect which is which.
If you are looking for a different system for crit hits/misses, that is one thing. But in the middle, 3d6 is just ... paint on the Porsche.
Willie the Duck
Legend
Is that all this is? If anyone can confirm, I just saved 120 posts of reading.
I don't think it's a surprise to anyone that gamers (as a trend) like to faff about with numbers, and sometimes the distinction isn't overly meaningful, but people still like to explore the ins and outs of them all. If you really want to meaningfully impact party success or failure, modifying what success entails* almost always will have a larger contribution than moving the likelihood of success by a minor amount.
*if categorical. Obviously in something like to-hit and damage whether changing the to-hit or the damage dealt has a higher contribution comes down to simple math.
One of my main GMs, when designing homebrew, loves to hand out +/- 1-3 %s for higher quality equipment, differing societal status in a social encounter, and so on, and I keep saying, "If even once during the game we convince you that we don't need to roll a check in a given situation, or you decide that a given challenge will require two checks instead of one, we've already wiped away any impact this will have." Guess what, he doesn't care? And he's probably right, psychologically -- Player 2 will still be excited about getting the +2% dagger and Player 3 will change their behavior to avoid the -1% to their roll (that puts their chance of success at the same place as it was last session before they upped their skill).
DC 14 with a +4 bonus.
3d6 passes on an 10 or better. So does a d20. Simple. Easy. Clean. Which one passes more often?
d20 passes on 55% of rolls
3d6 passes on 62% of rolls.
Hmm... there seems to be a discrepancy, here.
How about DC18 with a +4 bonus? They both need a 14 or better!
d20 passes on 35% of rolls.
3d6 passes on 16% of rolls.
WILD.
How about a DC of 5 with a +2 bonus? Only need a 3 or better!
d20 is a 90%
3d6 is 100% (99.54 if a 3 is an automatic failure, 98.15 if a 3 and 4 are automatic failures)
Okay, okay. That one's a bit cheatsy. Let's bump it up to DC 7 with a +2 bonus.
d20 is 75%
3d6 is 98%
DC 20 with a +4 bonus?
d20 is 25%
3d6 is 4% Charitably we could round up to a 5%.
Now, of course, you can adjust all the DCs of 5e D&D to conform to a 3d6 system... but most people who use 3d6 change absolutely nothing whatsoever other than which dice are being rolled. And especially early game, it means greater competence for PCs and NPCs when DCs and bonuses are lowest.
And late game, when the enemy's AC is 20 and you've got a +13 to the roll? (+6 Proficiency, +5 Attribute, +2 Weapon)
d20 70%
3d6 91%
How can you look at these values, these significant differences in chance to land the hit, and say there's no difference?
3d6 passes on an 10 or better. So does a d20. Simple. Easy. Clean. Which one passes more often?
d20 passes on 55% of rolls
3d6 passes on 62% of rolls.
Hmm... there seems to be a discrepancy, here.
How about DC18 with a +4 bonus? They both need a 14 or better!
d20 passes on 35% of rolls.
3d6 passes on 16% of rolls.
WILD.
How about a DC of 5 with a +2 bonus? Only need a 3 or better!
d20 is a 90%
3d6 is 100% (99.54 if a 3 is an automatic failure, 98.15 if a 3 and 4 are automatic failures)
Okay, okay. That one's a bit cheatsy. Let's bump it up to DC 7 with a +2 bonus.
d20 is 75%
3d6 is 98%
DC 20 with a +4 bonus?
d20 is 25%
3d6 is 4% Charitably we could round up to a 5%.
Now, of course, you can adjust all the DCs of 5e D&D to conform to a 3d6 system... but most people who use 3d6 change absolutely nothing whatsoever other than which dice are being rolled. And especially early game, it means greater competence for PCs and NPCs when DCs and bonuses are lowest.
And late game, when the enemy's AC is 20 and you've got a +13 to the roll? (+6 Proficiency, +5 Attribute, +2 Weapon)
d20 70%
3d6 91%
How can you look at these values, these significant differences in chance to land the hit, and say there's no difference?
Similar Threads
Recent & Upcoming Releases
-
June 16 2026 -
June 16 2026 -
September 16 2026 
Arcana Unleashed(Dungeons & Dragons)
Rulebook featuring "high magic" options, including a host of new spells.
Replies (239) -
September 16 2026 -
October 1 2026 -
October 6 2026 -
January 1 2027
