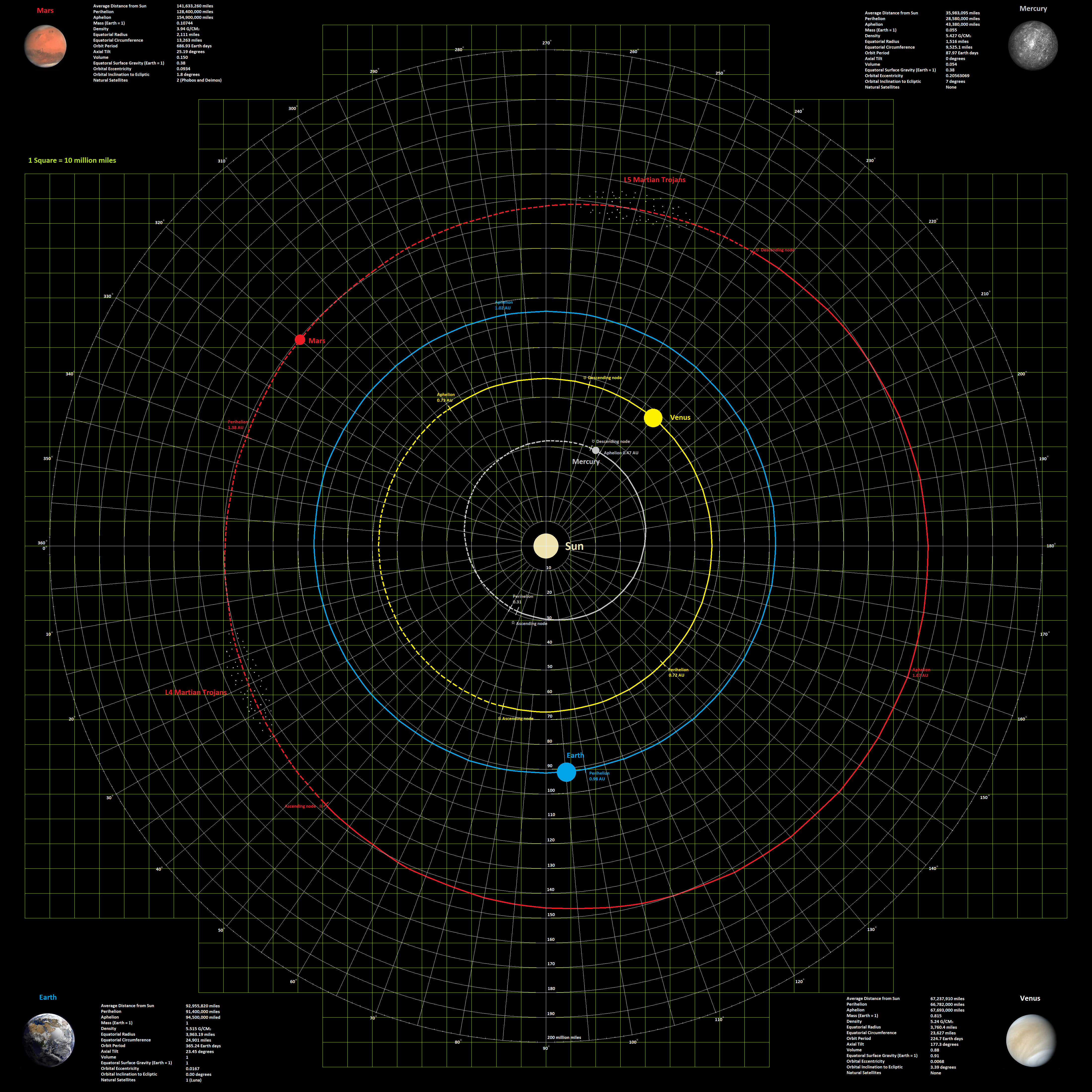
Here is a map of the Inner System:
Using the Realistic Travel times for D20 Future under the column for PL6 Engine we have the following Travel Times:
Earth to the Moon (240,000 miles) 8 hours
Earth to the Sun (93,000,000 miles) 129.2 days
Earth to Mercury (56,950,000 miles 79.1 days
Earth to Venus (26,040,000 miles) 36.2 days
Earth to Mars (48,360,000 miles) 67.2 days
We get a travel rate of 3 million miles every 100 hours. (4 and 1/6 days).
30,000 miles per hour.
48,000 km per hour.
13,333 and 1/3 meters per second
Lets assume an acceleration of 1 meter per second, that is 3.7 hours to accelerate to this velocity for a total of 7.4 hours of acceleration time for a total distance traveled at an average speed of 15,000 miles per hour, of 111,000 miles the remaining miles to be covered is 129,000 miles, which at a rate of 30,000 miles per hour takes an additional 4.3 hours for a total travel time of 11.7 hours.
So using the formula:
(Distance in miles - 111,000 miles) / 30,000 miles per hour + 7.4 hours = The travel time in hours.
One can find the distance in squares by the distance formula by counting the horizontal number of squares between two planets on the map, and then the vertical number of squares and then applying the Pythagorean theorem Distance = square root of the sum of the vertical distance squared and the horizontal distance squared or
Distance = (x^2 + y^2)^0.5
A more legible map can be found at
https://thomasbowman767.deviantart.com/art/Solar-System-Inner-725496454
The positions on the map can be used as the starting positions, the map I took them from shows the positions of the planets at the beginning of the year 2013, but for game purposes, you can either find the actual positions of the planets in the year 2078 or you can just use this map as is, however you like. We have a period for each orbit, so this gives you how many degrees to advance each planet for any given time period, or you can use Kepler's law of planetary motion, which states that a planet sweeps equal areas of its orbit in equal amounts of time. Area of a circle is Area = 2 pi radius^2. The period of the orbit of each planet is found at the corners of the map. Divide the area of a circle at the planet's average distance from the Sun by its orbital period in days, and that is the area swept out by each planet in one day, now use the current distance of the planet and calculate the distance covered by that planet when it sweeps an equal area of a circle drawn at the current distance. So if te current distance is greater than average, it will travel fewer degrees in one day, if it is closer, it will cover more degree in its orbit. All orbital motion on this map is counter-clockwise. Dotted line orbits indicate that portion of the orbit is below the plane of the ecliptic.