Haiku Elvis
Knuckle-dusters, glass jaws and wooden hearts.
I think the only way is to have successes be more than 1 per dice but that may defeat the purpose of a success or fail dice pool mechanic.
For example each six sided dice has 3 blank 0s and 1, 2 and 3 on the remaining faces.
That only leaves impossible rolls with a pool of 1 as two dice have a 1 in 36 chance of rolling two 3s to hit the 6 target.
Actually any one outcome on two dice is 1 in 36 so the example of a pool of 2 dice hitting a target of 4 would be 5 in 36 I think.
Wolfram Alpha can do the maths if you don't mind typing in the results one at a time.
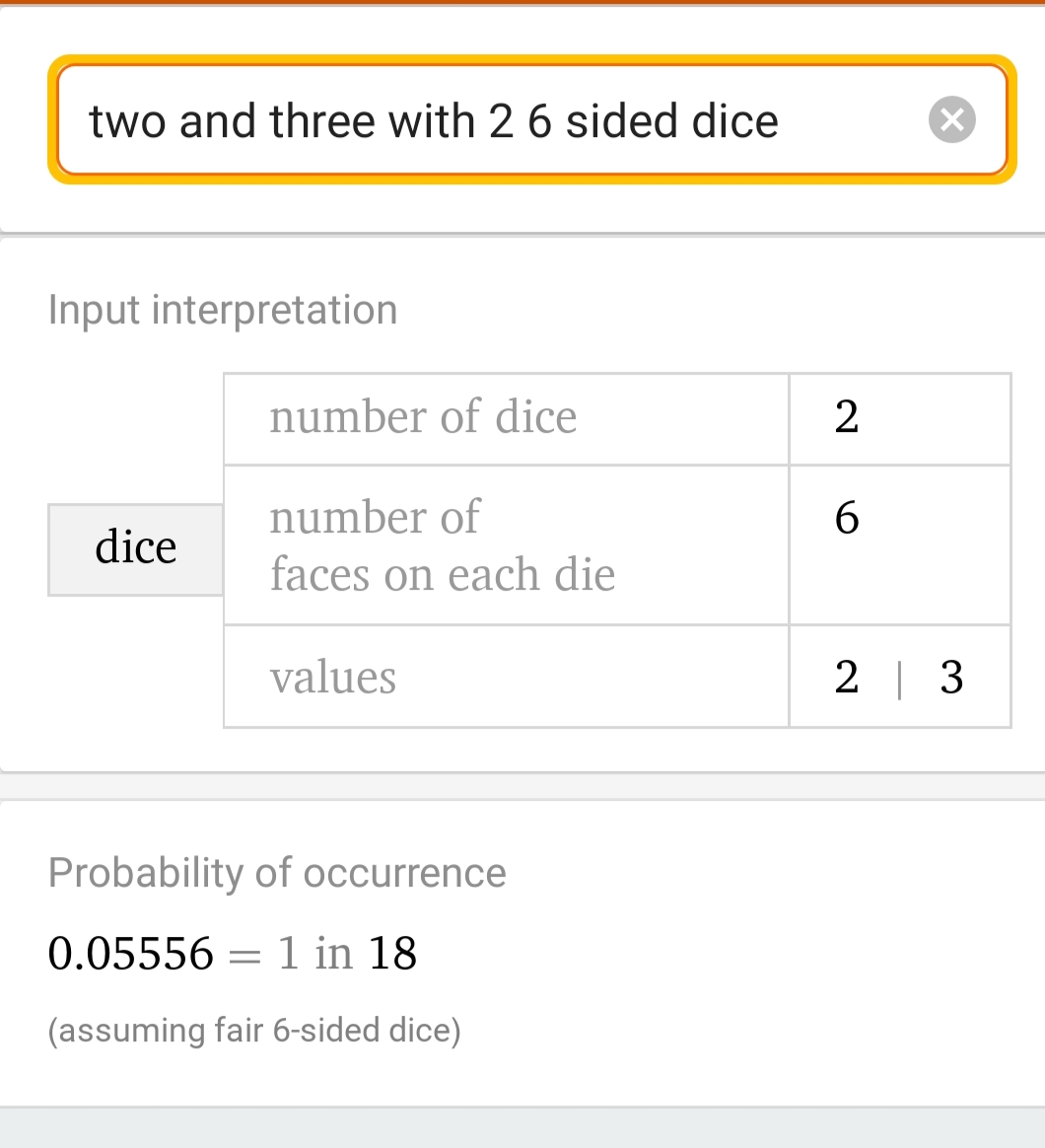
For example each six sided dice has 3 blank 0s and 1, 2 and 3 on the remaining faces.
That only leaves impossible rolls with a pool of 1 as two dice have a 1 in 36 chance of rolling two 3s to hit the 6 target.
Actually any one outcome on two dice is 1 in 36 so the example of a pool of 2 dice hitting a target of 4 would be 5 in 36 I think.
Wolfram Alpha can do the maths if you don't mind typing in the results one at a time.





