D&D Beyond's latest data-output looks at the composition of the typical adventuring party. The 'traditional' party always used to be Fighter, Cleric, Rogue, Wizard; let's see how that stacks up these days!
These screenshots were compiled by SageAdvice.eu. DDB's developer said "I’m going to be honest: this was really hard to look at from a data perspective right, so what I mean by that is it’s hard to figure out exactly how to chop this data up for it to be the most meaningful that we can make it all right. These are all campaigns where party members and characters within that campaign are taking hit point adjustments, so that’s one of the best senses that we have that something is actually being played”.


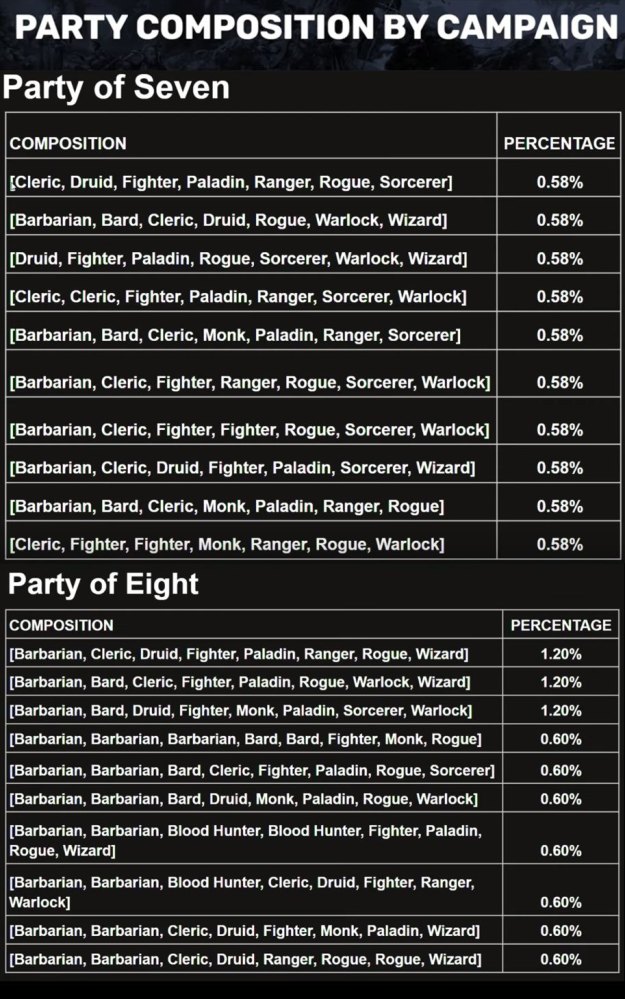
These screenshots were compiled by SageAdvice.eu. DDB's developer said "I’m going to be honest: this was really hard to look at from a data perspective right, so what I mean by that is it’s hard to figure out exactly how to chop this data up for it to be the most meaningful that we can make it all right. These are all campaigns where party members and characters within that campaign are taking hit point adjustments, so that’s one of the best senses that we have that something is actually being played”.




