D&D 4E Non-Euclidean Geometry in 4E?

[Benimoto]

Radius and reach are not the same thing.
The reach start from "all around" the attacker's square.
Radius is measured from a same point.

In the reach diagram, it makes perfectly sense that the attacker could hit the creature on the corner squares. It could at least affect 50% of the square in the corner, so it's enough to reach anyone there.

I'm too lazy/sleepy to bust out my calculus for an exact percentage, so we'll go with another visual representation. Those corner squares are less than 50% covered, and a 10-foot line doesn't even quite touch the center of the corner squares. (Which are what, around 10.6 feet away?)

I'm pretty sure that the corners being covered by 10-foot reach is just to prevent the anomaly where an attacker can approach from certain directions and not suffer attacks of opportunity.

In the radius diagram, the 'logical' 10ft. radius circle is really a little wider than that.
If you put a 10ft. radius circle on the grid, like I did in the last diagram, the actual 10ft radius circle works well. IIRC there is a rule (of thumb?) in D&D that says "if the area of the effect covers less than 50% of the area of a square, a creature in the square is not affected". That's what happens with the Actual 10'R circle.

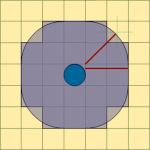
I agree, and it's more a symptom of the designers trying to use one mechanic to cover everything. 10-foot radii work fine for attack spells. It's only emanations that cover the caster where you get the logical breakdown, and it's because of the rule that all area effects (except reach) radiate from a specific corner. Personally, I don't know anyone who's tried to enforce this in the case of spells like Magic Circle Against Evil/whatever. Asking the caster to declare a corner every turn is silly. It's somewhat illogical that some people who are 10 feet away, or even 5 feet away from the target in certain cases, aren't covered in a 10-foot radius emanation, so every time I've seen the spell cast those mechanics get ignored.

There's still the issue with the 1-2-1-2 system that cones cover more area if you direct them "straight out" than "diagonally." Of course moving to a 1-1 system doesn't promise any answers there. It would just make things worse.

So anyways, I guess my point is that none of the systems are perfect. They all lead to strange unintuitive situations and weird exceptions. The 1-1 system has as its advantage that it's easier to count, and in my book, that's a pretty big advantage.

 

[Benimoto]

Further, not to pick on Ainatan here, who I believe to be a reasonable and persuasive fellow, but his example in post 47 is very slightly misleading. He is correct that in the 1-1-1-1 system, a monster can use the "diagonal dodge" to avoid attacks of opportunity.

But, neither the 1-2-1-2 or 1-1-1-1 system for diagonals fully protects the wizard. In both systems the monster can go around the fighter and attack the wizard while provoking attacks of opportunity.

 

[Mouseferatu]

Out of raw curiosity, why? I can understand preferring "diagonal = constant" to "diagonal = alternating 1 and 2" for gameplay speed reasons, but why do you have a preference for "diagonal = 1" over "diagonal = 2"?

Because whenever I have two options that are equally mechanically sound, I prefer the one that is

A) both more consistent with the other rules, and

B) least limiting to a character's (or monster's) options.

 

[BASHMAN]

If not counting 1,2,1,2 will melt your face on a square grid, why not switch to a hex grid. then it will never be an issue.

 

[Dausuul]

But, neither the 1-2-1-2 or 1-1-1-1 system for diagonals fully protects the wizard. In both systems the monster can go around the fighter and attack the wizard while provoking attacks of opportunity.

This is true, and even with hexes or offset squares this problem will exist to some extent; as long as we have granular movement (i.e., count off squares/hexes/whatevers rather than measuring the actual distance), there will be circumstances in which one can go around an obstacle and not lose any time by doing so.

However, the further the movement system diverges from reality, the more pronounced this effect becomes. In the 1-2 system, it's relatively rare and can be handwaved without much trouble. With hexes it's a bit more pronounced, mostly due to the weirdness of east-west movement. With one-for-one diagonals, however, it's glaringly obvious.

I just hope 4E's system is flexible enough to accommodate people using hexes or 1-2 movement. As long as I can house-rule it, I can deal.

 

[DMShoe]

It is faster and easier.

Even for experienced players.

I've got players who have been playing for years who would still forget to count the extra squares for diagonal movement. Sure, they'd sometimes remember if all their diagonal movement was contiguous, but if they moved one diagonal, then some orthogonal, then another diagonal, guess how often they'd remember to count "2" for that next diagonal.

And really, it ends up not being worth worrying about.

Mouseferatu's summed up a lot of relevant thoughts, and a lot of good thoughts and points have been brought up by others in this thread (which I"m sure will continue to get discussed and bury this post under the weight of the hex vs squares vs geometry discussion).

A thought I'll share, then let you return to your debate: when the change was first discussed, we touted many of the advantages of the 1.5-length diagonal - with many of the same arguments held in this thread. The thought of going to 1-1 created all sorts of wierd situations that didn't seem to sit well. But once we started playing? it didn't matter. It was clear. Ranges, areas, movement -- everyone understood how it worked, and we could focus on the more important parts of the game, like rolling dice and using powers and telling the story.

Will I miss 1-2-1? sure. primarily when I'm not playing, but thinking about the game. But after playing for a while, I'm more and more sure that most people aren't going to miss it, and their games are going to be better for it. And as Ari pointed out - you can houserule it back if you think it's that big of a deal.

Besides -- the defender who is trying to "defend" by standing in the middle of an open room isn't doing his job very well. Even with 1-2-1, the monster could move out to the side and then charge the wizard. The defender should either be back near the wizard, or basing the monster. Just sayin'.

 

[Dausuul]

A thought I'll share, then let you return to your debate: when the change was first discussed, we touted many of the advantages of the 1.5-length diagonal - with many of the same arguments held in this thread. The thought of going to 1-1 created all sorts of wierd situations that didn't seem to sit well. But once we started playing? it didn't matter. It was clear. Ranges, areas, movement -- everyone understood how it worked, and we could focus on the more important parts of the game, like rolling dice and using powers and telling the story.

Thanks for sharing your experiences with us. I'll have to ponder that.

Just curious: Did you try out hex-based combat? If so, did you find it more cumbersome than square-based? Obviously squares are somewhat more convenient for map-drawing in a "rectangular dungeon" setting, but assuming the DM is willing to cope with that, is there any other reason to go with 1-1 squares rather than hexes?

 

[DMShoe]

Out of raw curiosity, why? I can understand preferring "diagonal = constant" to "diagonal = alternating 1 and 2" for gameplay speed reasons, but why do you have a preference for "diagonal = 1" over "diagonal = 2"?

A quick note on this -- there is wierdness when you can attack a square next to you (without using a reach weapon), but can't also move into that square (when a corner or other obstruction isn't in the way). It's better (we think, at least) if you count range and movement and similarly as possible, therefore adjacent squares are always 1 square away. This also allows things like a radius-1 "burst" affect to hit all adjacent squares, and be simple to describe in the context of the game rules.

 

[Sammael]

Shoe,

I, for one, am certainly not questioning the speed and ease of the new rule. Of course it's faster and easier. But there is a moment when I started wondering if... well... speed and ease aren't everything. While it certainly makes sense to try and make the game run as smoothly as possible, to me, there is a certain point when the suspension of disbelief is no longer possible because of abstraction. And believe me, I've been defending abstraction in D&D to players of other systems for YEARS.

Curiously enough, one of the people I know who hates D&D saw this change and commented that it was great. When I asked him why, he said "Because they're no longer even pretending D&D is an RPG - they've gone boardgame all the way." You can imagine that comment left a bitter aftertaste.

I'll be switching to hexes for my next campaign.

 

[spalk]

Well, I do find it quite surprising, that so many people find it so cumbersome to use the "1-2-1-2"-rule, we have never had any problems with it. It is probably faster to go "1-1-1-1", but...I suppose that I feel sympathy with the original poster here.

But this doesn't really have anything to do with Non-Euclidean Geometry. Even in Neutral Geometry, the triangle inequality holds (and the criterion for equality), so the diagonals of a square are longer than its sides.