Hypersmurf
Moderatarrrrh...
The distance however, is between the combatants, not between squares beside the combatants.
No, it isn't. He doesn't need to move to the combatant. He needs to move to the nearest square from which he can attack the combatant.
The distance we need to measure is the distance between the charger, and the nearest square from which he can attack the target. Not the distance between the charger and the target.
Let's say we have an open field, no corners in sight. Our charger has a longspear. He has a speed of 6 squares. His target is 8 squares away.
Can he charge? Certainly. Because the distance he needs to move is 6 squares - the distance between where he is, and the nearest square from which he can attack the target. The figure of 8 squares is completely irrelevant, because we don't care about the distance between where he is and where the target is. He isn't moving there.
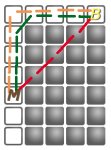
Let me redraw the monkey scenario and see if it helps you see what I'm saying:
Code:
--------
--abcdB--
--M#####
---#####
---#####
---#####What is the distance from the monkey to the banana?
When counting the distance from one square to another, start counting from any adjacent square (even one that is diagonally adjacent but around a corner) and then count around solid obstacles that fill their squares.
I start counting from a square adjacent to the monkey (even one that is diagonally adjacent but around a corner). That's square b.
So the squares I count are b, c, d, and the banana's square. The distance is 4.
What's the distance from square a to the banana?
I start counting from a square adjacent to the square a (even one that is diagonally adjacent but around a corner). That's square b.
So the squares I count are b, c, d, and the banana's square. The distance is 4.
So if the monkey moves to square a, his distance to the banana is unchanged. He has not moved towards the banana - he's moved laterally, to use your phrase.
(Of course, as I said before, he's not actually moving to the banana, he's moving to square d. But the logic's the same - from his initial position, it's three squares to square d. From square a, it's three squares to square d. Moving to square a is not moving towards square d.)
-Hyp.
Last edited: