DND_Reborn
The High Aldwin
Today I was thinking about the standard array (15, 14, 13, 12, 10, 8) and point-buy compared to rolling ability scores using the suggested 4d6, drop lowest because, well, I am a nerd and have free time now. 
First, the average for standard array is 12, while the average for point-buy ranges from 11.5 - 12.5, averaging 12.05 roughly if you consider all possible sets. IME, however, point-buy has a slightly higher average overall in use, about 12.2 or so. Finally, rolling 4d6, drop lowest, has an average of 12.24.
I am looking for methods that have an average of roughly 12-12.5, the closer to 12.25 the better, that will randomly generate scores from 8 - 15.
I have some ideas (see spoiler's below) for methods for rolling scores from 8 to 15, inclusive, because our group likes the range offered by the standard array and point-buy, and we find when players do roll 4d6, drop lowest, their scores tend to be too good. But we have some players who love to roll their ability scores, so I am trying to develop a method for them.
What can you come up with that is (hopefully) simple, generates scores from 8 - 15, and averages about 12.25 or so? Any ideas?
If you look at the spoiler, are any of the methods I have more appealing to you personally?
Finally, if you have a method you've developed for determining ability scores and wish to share it, please do!
First, the average for standard array is 12, while the average for point-buy ranges from 11.5 - 12.5, averaging 12.05 roughly if you consider all possible sets. IME, however, point-buy has a slightly higher average overall in use, about 12.2 or so. Finally, rolling 4d6, drop lowest, has an average of 12.24.
I am looking for methods that have an average of roughly 12-12.5, the closer to 12.25 the better, that will randomly generate scores from 8 - 15.
I have some ideas (see spoiler's below) for methods for rolling scores from 8 to 15, inclusive, because our group likes the range offered by the standard array and point-buy, and we find when players do roll 4d6, drop lowest, their scores tend to be too good. But we have some players who love to roll their ability scores, so I am trying to develop a method for them.
Method #1 is a simple d8 + 7, but this produces an average of only 11.5, and given the linear nature is not as appealing.
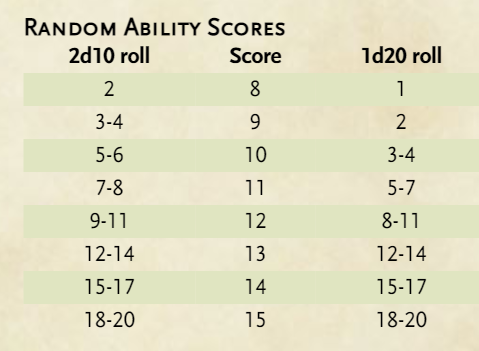
Method #2 and 3 involve rolling either 2d10 or 1d20, respectively, and consulting the chart. The averages are 12.22 and 12.2, so that is good, but I am not a fan of consulting a chart for such purposes.
Method 4 involves rolling both 1d6 and 1d8, taking the best roll, and adding 7. This allows for rolling and doesn't require the chart, is non-linear although is skewed, and has a good average of 12.23. But, the idea of rolling dice of two different sizes is somewhat off-putting.
Method #2 and 3 involve rolling either 2d10 or 1d20, respectively, and consulting the chart. The averages are 12.22 and 12.2, so that is good, but I am not a fan of consulting a chart for such purposes.
Method 4 involves rolling both 1d6 and 1d8, taking the best roll, and adding 7. This allows for rolling and doesn't require the chart, is non-linear although is skewed, and has a good average of 12.23. But, the idea of rolling dice of two different sizes is somewhat off-putting.
What can you come up with that is (hopefully) simple, generates scores from 8 - 15, and averages about 12.25 or so? Any ideas?
If you look at the spoiler, are any of the methods I have more appealing to you personally?
Finally, if you have a method you've developed for determining ability scores and wish to share it, please do!
