You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Science: asteroid vs. hero physics
- Thread starter Janx
- Start date
Would a cascade of multiple pick bullets be better than one punch through? She collects multiple debris bullets drags them in orbit around the planet and sets them all to collide with the asteroid ....
Momentum is effectively mass * velocity. Multiple impacts aren't "better" than a single impact in the sense that you need at *least* as much momentum transfer from the multiple impacts as you do from a single impact. I say at least because the velocity you need to impart grows the closer the target gets to Earth so time to impact matters a lot. If you can set up a single impact to hit at 1 minute, and multiple impacts, the last of which hits at one minute, then the multiple impact option might be better if you have an easier time arranging multiples, say for example, your suit can only accelerate a few tonnes at a time. If you only have an hour to disaster then if time to final impact is 10 minutes, you will probably need to accelerate substantially more mass than a single hit at one minute. The other issue is you'll have to set up the shots guessing about how the earlier shots will affect the target. It's size isn't very large in the scheme of things and small uncertainties in its mass could easily lead to complete misses of your later shots.
With a much longer time horizon, multiple impacts can be much more useful in the sense that you get small changes with each impact and those changes could lead to having more time available. Multiple impacts might also allow you time to reevaluate and to recover from a mishap more easily. You also reduce the possibility of secondary unfortunate consequence -- like say breaking the object into two and needing to prevent both parts from striking or responding to a miss/unexpected result.
tomBitonti
Hero
I disagree. The problem here is the same one you make about -- when you shifted the frame from the road/field to the car, you DON'T shift the vector of the wind -- it remains the same. Ergo, if you go with an Earth centric reference frame, the asteroid's motion is actually comprised of it's vector and the Earth's speed vector, creating the apparent straight line movement towards Earth. If you restart the Earth, you don't change the Asteroid's original vector, you just recover the Earth's vector back to Earth. The push that was perpendicular in the Earth frame is still in the same direction, which is now diagonal to the asteroid's path. This means you're both slowing the asteroid AND pushing it to the side. At 5 minutes out, the breakpoint speed where slowing becomes more efficient than pushing it to the side is:
This seems to be both agreeing and disagreeing: In the earth centric frame, the push is perpendicular to the motion of the asteroid in that frame. That same push, when transormed into a sun centered frame, can be as you say, mostly speeding up or slowing down the asteroid, and just a little to the side, depending on the relative motions of the earth and of the asteroid.
The reason for using an earth centered frame of reference is that the problem and the resulting maths are much simpler.
A theme here which is important is that there is no special (“distinguished”) frame of reference. Just more and less natural and more and less useful ones.
In this problem, in the Earth frame of reference, is seems much simpler to find the most efficient push to give to the asteroid. Once that most efficient push is determined, it’s simple to transform to other frames of interest, say, a sun centered frame, or a frame that moves with the asteroid.
Thx!
TomB
tomBitonti
Hero
Would a cascade of multiple pick bullets be better than one punch through? She collects multiple debris bullets drags them in orbit around the planet and sets them all to collide with the asteroid ....
Lots of small pushes instead of one big one. That seems safer in not causing the asteroid to shatter.
But, it would still very likely be overwhelmed by the hugeness of the asteroid. I wonder - over how much area must the push be spread to stay within the strength of material of the asteroid?
Thx!
TomB
Lots of small pushes instead of one big one. That seems safer in not causing the asteroid to shatter.
But, it would still very likely be overwhelmed by the hugeness of the asteroid. I wonder - over how much area must the push be spread to stay within the strength of material of the asteroid?
Thx!
TomB
plus I have to consider how much mass is floating up in orbit and how much time it takes to scoop up. Scooping up a shredded ISS might be feasible.
It sounds like we're back to the perpendicular push per Ovinomancer's corrected math.
If she can scoop up enough material and turn it into a big mass driver(TM) mounted on the side of the asteroid, that solves the fiction vs. physics of big numbers. We could make the risk be that she has to power it, and it's gonna be close with her back to the earth as it scrapes by.
tomBitonti
Hero
plus I have to consider how much mass is floating up in orbit and how much time it takes to scoop up. Scooping up a shredded ISS might be feasible.
It sounds like we're back to the perpendicular push per Ovinomancer's corrected math.
If she can scoop up enough material and turn it into a big mass driver(TM) mounted on the side of the asteroid, that solves the fiction vs. physics of big numbers. We could make the risk be that she has to power it, and it's gonna be close with her back to the earth as it scrapes by.
With a mass driver you could scoop up stuff from the asteroid itself!
That would work for a distant asteroid, but doesn’t seem to work for an an asteroid which is at most a day away.
Thx!
TomB
MarkB
Legend
So, this molecular 3D-printing stuff, how sophisticated and how quick is it? One option would be to use it to break down matter on the asteroid, turn it into pico-printer-gel manufacturers, and then use those in turn to break down more of it, in an exponential replication loop. Once the whole thing is turned into printers, they then turn each other into propulsion units and fly themselves away.
tomBitonti
Hero
Starting with:
That doesn't have enough detail. Further basic results are also lacking in deail.
Finally:
Assessments of the energy, mass and size of the Chicxulub Impactor
Hector Javier Durand-Manterola and Guadalupe Cordero-Tercero
Departamento de Ciencias Espaciales, Instituto de Geofísica, Universidad Nacional
Autonoma de México
Arxiv March 19, 2014
Since our hero was having difficulty with a much smaller rock having a
diameter of 1km, the following uses the lowest values from the ranges
of the estimate:
Diameter
1.06 10^4 m
Mass:
1.0 10^15 kg
Kinetic Energy (KE):
1.3 10^24 J
Then:
Volume:
6.2 10^11 m^3
Density:
1.6 10^3 kg/m^3
Speed:
5.1 10^4 m/s (51 km/s)
In support of these values, Assessments writes:
Motion of 51 km/s is 1.84x10^5 km/hr, or 4.4x10^6 km/day.
(In comparison, Earths average orbital speed is about 30 km/s.)
Working from the equations of motion under constant acceleration,
and that relate force, mass, and acceleration:
Under constant acceleration:
D = 1/2 A T^2
Or:
A = 2 D / T^2
Definition of force:
F = M A
Then:
A = F / M
From which:
F / M = 2 D / T^2
Or:
F = 2 D M / T^2
Putting in:
The radius of the Earth:
D = 6.4x10^6 m
The mass of the asteroid:
M = 1.0 10^15 kg
The available time (one hour):
T = 3.6 10^3
Results in:
F = 1.0 10^15 kg m / s^2
Total impulse is:
I = F T
I = 3.6 10^18 kg m / s
From: http://www.b14643.de/Spacerockets_2/United_States_1/Saturn-5/Design/SaturnV.htm
The total impulse of the Saturn V for Apollo 17 (launched 12-Jul-1972) was:
I(SV) = 8.7x10^9 kg m / s
That is, pushing the asteroid out of the way would require the total
impulse of 2.4x10^8 (240,000,000, or 240 million) Saturn V's.
Notes:
The impulse requirements do not vary with the speed of the asteroid!
What matters is how long one has to push the asteroid out of the way.
That this should be the case can be seen by adopting an asteroid-centric
frame of reference, in which case the asteroid is still and
the earth which is in motion. When looked at from this frame of
reference, all that matters is how long until the Earth and the
asteroid collide, not how fast the earth is moving.
From the force and total impulse equations:
F = 2 D M / T^2
I = F T = 2 D M / T
The force requirement increases linearly with the distance and mass,
and decreases in portion to the square of the available time. But,
the total impulse requirement decreases linearly with the available
time. (That is, as the available time increases, while the necessary
force is reduced, the duration of application of that force increases,
moderating a square factor to a linear one.)
Requirements for an asteroid having a similar composition but having a
different radius vary according to the change of radius of the
asteroid. Changing from 10km to 1km reduces the force requirement by
a factor of 1000 (10^3). Note that a "small" 1 km asteroid, still
needs the total impulse of 240,000 Saturn V's.
Thx!
TomB
https://en.wikipedia.org/wiki/Chicxulub_impactor said:the Chicxulub asteroid, was an asteroid or other celestial body some
10 to 15 kilometres (6 to 9 mi) in diameter
That doesn't have enough detail. Further basic results are also lacking in deail.
Finally:
Assessments of the energy, mass and size of the Chicxulub Impactor
Hector Javier Durand-Manterola and Guadalupe Cordero-Tercero
Departamento de Ciencias Espaciales, Instituto de Geofísica, Universidad Nacional
Autonoma de México
Arxiv March 19, 2014
https://arxiv.org/ftp/arxiv/papers/1403/1403.6391.pdf said:... the aim of this study is to estimate the most relevant features of
this one such as the size, mass and kinetic energy. We found that the
kinetic energy of the impactor is in the range from 1.3x10^24 J to
5.8x10^25 J. The mass is in the range of 1.0x10^15 kg to 4.6x10^17
kg. Finally, the diameter of the object is in the range of 10.6 km to
80.9 km.
Since our hero was having difficulty with a much smaller rock having a
diameter of 1km, the following uses the lowest values from the ranges
of the estimate:
Diameter
1.06 10^4 m
Mass:
1.0 10^15 kg
Kinetic Energy (KE):
1.3 10^24 J
Then:
Volume:
6.2 10^11 m^3
Density:
1.6 10^3 kg/m^3
Speed:
5.1 10^4 m/s (51 km/s)
In support of these values, Assessments writes:
In the second model, to calculate the kinetic energy of the impactor,
we needed crater diameter, density of the projectile, density of the
target, earth's gravity and impactor velocity. We considered the
density of the projectile as 1650 kg/m^3 for comets (Greenberg, 1998),
3400 kg/m^3 for stony asteroids (Wilkison and Robinson, 2000), and
8000 kg/m^3 iron asteroids (Hills and Goda, 1993). We took the target
density as 2460 kg/m^3, which is the modal density of the limestone of
Yucatan (Alonzo et al., 2003), and Earth's gravity as 9.80 m/s^2
(Tholen et al., 2000). Steel (1998) obtain ed an estimation of the
range of velocities for bodies that cross Earth's orbit. For asteroids
the interval is between 12.6 km/s and 40.7 km/s. This result is based
on measurements of the velocities of the asteroids that cross Earth's
orbit.
The range for comets is between 16 km/s and 73 km/s. This result is
obtained from a theoretical calculation of the expected velocity
distribution of bodies that come from the Öpik-Oort cloud.
Motion of 51 km/s is 1.84x10^5 km/hr, or 4.4x10^6 km/day.
(In comparison, Earths average orbital speed is about 30 km/s.)
Working from the equations of motion under constant acceleration,
and that relate force, mass, and acceleration:
Under constant acceleration:
D = 1/2 A T^2
Or:
A = 2 D / T^2
Definition of force:
F = M A
Then:
A = F / M
From which:
F / M = 2 D / T^2
Or:
F = 2 D M / T^2
Putting in:
The radius of the Earth:
D = 6.4x10^6 m
The mass of the asteroid:
M = 1.0 10^15 kg
The available time (one hour):
T = 3.6 10^3
Results in:
F = 1.0 10^15 kg m / s^2
Total impulse is:
I = F T
I = 3.6 10^18 kg m / s
From: http://www.b14643.de/Spacerockets_2/United_States_1/Saturn-5/Design/SaturnV.htm
The total impulse of the Saturn V for Apollo 17 (launched 12-Jul-1972) was:
I(SV) = 8.7x10^9 kg m / s
That is, pushing the asteroid out of the way would require the total
impulse of 2.4x10^8 (240,000,000, or 240 million) Saturn V's.
Notes:
The impulse requirements do not vary with the speed of the asteroid!
What matters is how long one has to push the asteroid out of the way.
That this should be the case can be seen by adopting an asteroid-centric
frame of reference, in which case the asteroid is still and
the earth which is in motion. When looked at from this frame of
reference, all that matters is how long until the Earth and the
asteroid collide, not how fast the earth is moving.
From the force and total impulse equations:
F = 2 D M / T^2
I = F T = 2 D M / T
The force requirement increases linearly with the distance and mass,
and decreases in portion to the square of the available time. But,
the total impulse requirement decreases linearly with the available
time. (That is, as the available time increases, while the necessary
force is reduced, the duration of application of that force increases,
moderating a square factor to a linear one.)
Requirements for an asteroid having a similar composition but having a
different radius vary according to the change of radius of the
asteroid. Changing from 10km to 1km reduces the force requirement by
a factor of 1000 (10^3). Note that a "small" 1 km asteroid, still
needs the total impulse of 240,000 Saturn V's.
Thx!
TomB
freyar
Extradimensional Explorer
I disagree. The problem here is the same one you make about -- when you shifted the frame from the road/field to the car, you DON'T shift the vector of the wind -- it remains the same. Ergo, if you go with an Earth centric reference frame, the asteroid's motion is actually comprised of it's vector and the Earth's speed vector, creating the apparent straight line movement towards Earth. If you restart the Earth, you don't change the Asteroid's original vector, you just recover the Earth's vector back to Earth. The push that was perpendicular in the Earth frame is still in the same direction, which is now diagonal to the asteroid's path. This means you're both slowing the asteroid AND pushing it to the side. <snip>
You certainly do shift the vector of the wind. But the main point I wanted to make is that you certainly can work in the earth's frame of reference without worrying about pseudo-forces over short time periods, and you now seem to be doing that. I think you have some assumptions hidden in your calculations, so I can't really comment on those.
In the earth's frame, you need some component of the push perpendicular to the asteroid's travel, but you're right that the optimal push isn't quite perpendicular. I don't have time to type out my work now, but I think the max deflection for an instantaneous impulse of magnitude dp on an asteroid of momentum p has sin(x)=dp/p, where x is the angle of the push from perpendicular to the asteroid velocity.
Ovinomancer
No flips for you!
You don't shift the wind. Unless and until you rotate the diagram, in which case you shift the wind, but rotation doesn't work well in this case because Earth is so big and the impact point, while appearing to be in line with Earth's center in one frame isn't in another. Here's a to scale diagram showing Earth as the circle on the left of a diameter including 150km of atmo (so it rounds up to a nice 13,000km diameter) and three asteroids (20km/s, 30km/s, 50km/s) at one hour from impact. This shows the travel of Earth in that time and the travel of the asteroids in that time in both the Solar frame (Earth moving up, asteroids moving left) and the Earth frame (diagonal asteroid paths). The grey arrow is the direction of an example push so that it's apparent that the shift in frame doesn't rotate the push. As you can see, you can't just rotate the Earth frame because the asteroids aren't moving towards Earth's center but instead a point on the circumference, and that circumference is so large you can't ignore it for the purposes of the example.You certainly do shift the vector of the wind. But the main point I wanted to make is that you certainly can work in the earth's frame of reference without worrying about pseudo-forces over short time periods, and you now seem to be doing that. I think you have some assumptions hidden in your calculations, so I can't really comment on those.
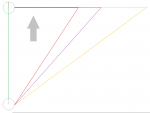
You must mean angle from the vector of the asteroid's travel, because otherwise a 90 degree push would be sin(0)=0.In the earth's frame, you need some component of the push perpendicular to the asteroid's travel, but you're right that the optimal push isn't quite perpendicular. I don't have time to type out my work now, but I think the max deflection for an instantaneous impulse of magnitude dp on an asteroid of momentum p has sin(x)=dp/p, where x is the angle of the push from perpendicular to the asteroid velocity.
That accounted for, the issue here is obvious when you consider it. The maximum dp occurs at sin(+/-90), but it would obviously require a much, much harder push if you went past 90 to generate a miss if you pushed from any angle behind the asteroid (ie, speeding it up while you generate a lateral velocity) but your formula has dp dropping off, not increasing. Also, it's possible to generate a miss by accelerating the asteroid "ahead" of the Earth, but your formula says needed dp there is 0.
I agree, there's an angle that minimizes pushed needed, but your assumption doesn't do it. Momentum is the wrong frame of thinking, as the asteroid's mass is constant so it falls out of the equations and you're just dealing with velocities. This is how most orbital problems work -- you deal in delta-v not momentum change. The challenge here is the point of impact being on the surface of a large circle instead of the center in the Earth frame, so the math gets messy. In the solar frame, it's two quickly moving objects. The math doesn't resolve into a simple sine equation.
Attachments
Similar Threads
Spoilers
Fantastic Four (Spoilers)
- Replies
- 108
- Views
- 11K
- Replies
- 51
- Views
- 10K
- Replies
- 8
- Views
- 6K
- Replies
- 101
- Views
- 18K
- Replies
- 1
- Views
- 2K
Enchanted Trinkets Complete
Recent & Upcoming Releases
-
December 9 2025 -
June 18 2026 -
October 1 2026



